6.2 Two methods for conducting a hypothesis test (when \(\sigma\) is known)
We will consider two equivalent methods for conducting a hypothesis test. The first is called the rejection region method and is very similar to confidence intervals. The second is the p-value method and delivers some very useful results that we will be using for the rest of the course. We will consider these methods in turn.
6.2.1 Rejection Region Method
All hypothesis tests start with a statement of the null and alternative hypotheses. The null makes an explicit statement regarding the value of a population parameter \((\mu)\). Once this value of \(\mu\) is established under the null, all hypothesis tests construct a test statistic under the null. In particular, assuming we know the population standard deviation \(\sigma\), we can construct a Z statistic under the null using our familiar z-transformation:
\[Z = \frac{\bar{X}-\mu}{\left(\sigma / \sqrt{n} \right)}\]
Note that we already know values from the sample \((\bar{X},\;n,\;\sigma)\) and we have a hypothesized value of \(\mu\) from the null hypothesis. We can therefore directly calculate this Z-value under the null. This would be the value of a Z-statistic given our sample characteristics under the assumption that our null hypothesis is correct.
The rejection region method takes this Z-statistic under the null and sees where it falls in a standard normal sampling distribution. The sampling distribution of a test statistic is first divided into two regions…
A region of rejection (a.k.a., critical region) - values of the test statistic that are unlikely to occur if the null hypothesis is true.
A region of nonrejection - values of the test statistic that are likely to occur if the null hypothesis is true, so they are consistent with the null hypothesis.
The regions of rejection and nonrejection are identified by determining critical values of the test statistic. These are particular values of the sampling distribution that divides the entire distribution into rejection and nonrejection regions. This is why some people refer to the rejection region approach as the critical value approach.
Once the different regions are established, then you simply see where the calculated test statistic under the null falls. If it falls inside the rejection region, then you reject the null because the characteristics of the sample are too inconsistent with the population parameter stated inside the null hypothesis. If it falls inside the nonrejection region, then you do not reject the null because the characteristics of the sample are such that the population parameter stated inside the null is possible (but we can’t say if it’s necessarily true).
The Steps of a Hypothesis Test (Rejection Region Method)
State the null and alternative hypotheses
Calculate a test statistic under the null
Determine the rejection and nonrejection regions of a standardized sampling distribution
Conclude (reject or do not reject)
Application 1
Suppose a fast-food manager wants to determine whether the waiting time to place an order has changed from the previous mean of 4.5 minutes. We want to see if our sample characteristics are consistent with an average of 4.5 minutes or not. We start with a statement of the two hypotheses.
\[H_0:\mu=4.5 \quad versus \quad H_1:\mu\neq 4.5\]
The null explicitly states that \(\mu=4.5\), so we can use this value to construct a test statistic using the information from our sample. Suppose that a sample of \(n=25\) observations delivered a sample mean of \(\bar{X}=5.1\) minutes. Suppose further that we know the population standard deviation of the wait time process to be \(\sigma=1.2\). We can calculate a test statistic under the null.
mu = 4.5
Xbar = 5.1
Sig = 1.2
n = 25
(Zstat = (Xbar - mu)/(Sig/sqrt(n)))## [1] 2.5\[ Z = \frac{\bar{X}-\mu}{\left(\sigma / \sqrt{n} \right)} = \frac{5.1-4.5}{\left(1.2 / \sqrt{25} \right)} = 2.5\]
The next step involves taking a standard normal sampling distribution and breaking it up into regions of rejection and nonrejection. Before we do this, lets take a step back and think about what it means for a sample to be consistent or inconsistent with the null hypothesis. If you had a sample average \((\bar{X})\) that was the same value as the parameter value stated in the null hypothesis \((\mu)\) then you could state that the value of \(\mu\) in the null hypothesis is very consistent with the characteristics of the sample. In fact, you can’t be more consistent than having \(\bar{X}\) and \(\mu\) being the exact same number. Furthermore, a test statistic under the null would be equal to zero because \((\bar{X}-\mu)\) is in the numerator. This implies that a test statistic under the null equal to zero is very consistent with the null hypothesis, and you will therefore not reject the null hypothesis. However, the farther away the test statistic under the null gets from zero, the farther away it gets from the center of the do not reject region and the closer it gets to one of the rejection regions.
Lets illustrate this supposing that we want to test the hypothesis at the 95% confidence level \((\alpha=0.05)\). The central 95% of a standard normal distribution is given by
\[Pr(-1.96 \leq Z \leq 1.96) = 0.95\]
This means that if you reached into a bowl of numbers comprising a standard normal distribution, then 95% of the time you will draw a number between -1.96 and 1.96. The remaining numbers outside of this range will show up only 5% of the time. These regions are the bases for confidence intervals and also the bases for the nonrejection and rejection regions.
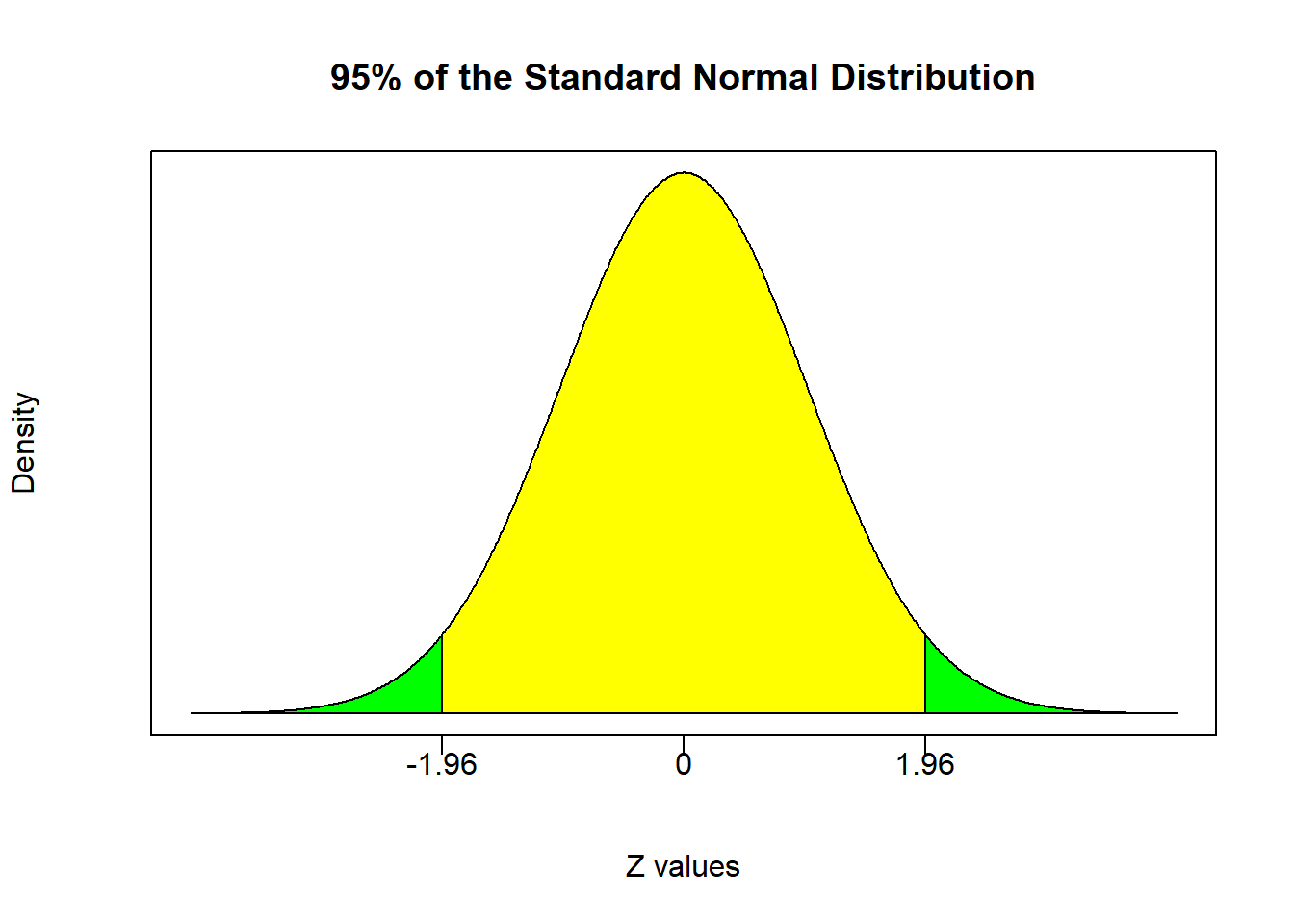
The yellow-shaded region is centered on zero and represents the nonrejection region. It tells you that if you calculate a test statistic under the null to be between -1.96 and 1.96, then you do not have enough evidence to reject the null. However, the green-shaded regions are the rejection regions. It tells you that if you calculate a test statistic under the null that is greater than 1.96 or less than -1.96, then you have enough evidence to reject the null (with 95% confidence). In other words, it is so unlikely to have the null be correct while simultaneously randomly selecting a sample with the observed sample characteristics, so we conclude that the statement in the null cannot be true. In the fast food example above, the test statistic under the null of 2.5 falls in the rejection region. This means that we can reject the null hypothesis of \(\mu=4.5\) minutes with 95% confidence. In other words, we are 95% confident that the population mean is some number other than 4.5 minutes.
Changing the level of confidence \((\alpha)\)
The hypothesis test above was concluded under a specified 95% confidence level \((\alpha=0.05)\). This level of confidence effectively delivered our rejection and nonrejection regions. So… what happens when we change \(\alpha\)?
The first thing to understand is that the level of confidence does not impact the hypotheses or the test statistic under the null. The only thing the level of confidence impacts is the shaded regions in the sampling distribution. The figure below illustrates rejection and nonrejection regions for \(\alpha\) values of 0.10, 0.05, and 0.01. Note that as \(\alpha\) gets smaller, the size of the nonrejection region gets larger. This means that do not reject is becoming a more likely conclusion. This should make sense because do not reject is a wishy-washy conclusion, while reject is definitive. Do not reject states that the null may or may not be true - it’s a punt! Therefore, if you are placing more confidence on your conclusion, the more likely you are to make the wishy-washy conclusion.
The fast food example had a test statistic under the null of 2.5. This test statistic falls in the rejection region for both 90% and 95% levels of confidence. This suggests that if you can reject a null hypothesis with a certain level of confidence, then you can automatically reject at all lower levels of confidence. However, the do not reject region under 99% confidence is given by \[Pr(-2.58 \leq Z \leq 2.58)=0.99\] and our test statistic of 2.5 falls inside it. We therefore conclude that we do NOT reject the null with 99% confidence. In other words, we do not have enough evidence to say that the null hypothesis is incorrect at 99% confidence, so we conclude that it may or may not be true (i.e., we punt).
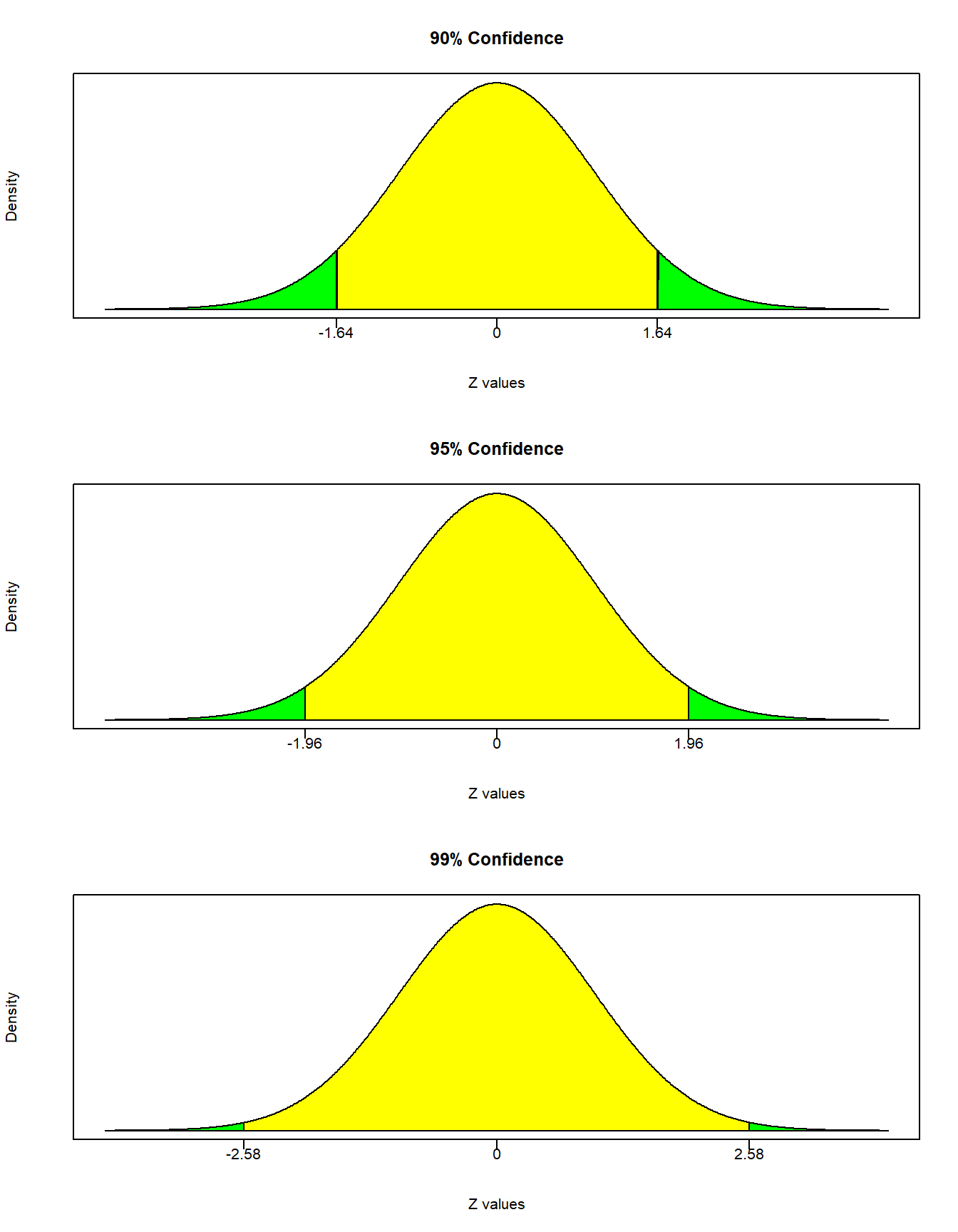
Using the rejection region method, we were able to reject the null with 95% confidence \((\alpha=0.05)\) but unable to reject with 99% confidence \((\alpha=0.01)\). This begs the question as to the highest confidence level at which we can reject the null. We know it is some confidence level between 95% and 99%, but what is it exactly? We can use the rejection region approach multiple times by choosing various values of \(\alpha\) and narrow things down, or we can conduct the hypothesis test using the p-value approach.
6.2.2 P-value Approach
The P-value is an extremely useful and often misunderstood number. I therefore have THREE equivalent ways of explaining it. Each one works - so just stick with the one that works for you. Before we get to those, lets talk explicitly about what we mean when we make statements based on confidence.
When using a sample statistic to draw conclusions about a population parameter, there is always the risk of reaching an incorrect conclusion. In other words, you can make an error.
When making a conclusion about a hypothesis test, one can either reject a null hypothesis or not. Therefore, there are two possible types of errors to be made.
A Type I error occurs when a researcher incorrectly rejects a true hypothesis. (You rejected something that shouldn’t have been rejected.)
A Type II error occurs when a researcher incorrectly fails to reject a false hypothesis. (You did not reject something that should have been rejected.)
The acceptable probability of committing either one of these errors depends upon an arbitrary confidence level \(\alpha\). To be precise, when you reject a hypothesis with 95% confidence, then you are implicitly stating that you are accepting a 5% chance of being wrong. That is where \(\alpha=0.05\) (or 5% comes from). If you decrease \(\alpha\) to 0.01 (or 1%), then you can reject a hypothesis with 99% confidence and implicitly accept a 1% chance of being wrong. The kicker is that the more you decrease the probability of committing a type I error, the more you increase the chance of not rejecting a hypothesis that you should be rejecting (a type II error). For example, if you want a conclusion with 100% confidence, then you will never reject a hypothesis no matter how wrong it actually is.7
The main take away from the previous statement is that \(\alpha\) states the acceptable probability of committing a type one error. Recall in our fast food example that we rejected the null hypothesis with 95% confidence (i.e., a 5% acceptable probability of being wrong ), but we did not reject the null hypothesis with 99% confidence (i.e., a 1% acceptable probability of being wrong ). This means that the actual probability of committing a type one error is somewhere in between 0.05 and 0.01 (i.e., 5% and 1%). This actual probability of committing a type I error is called the p-value.
# Fast Food Example Revisited
mu = 4.5
Xbar = 5.1
Sig = 1.2
n = 25
(Zstat = (Xbar - mu)/(Sig/sqrt(n)))## [1] 2.5# 95% confidence:
alpha = 0.05
(Zcrit = qnorm(alpha/2,lower.tail = FALSE))## [1] 1.959964# 99% confidence:
alpha = 0.01
(Zcrit = qnorm(alpha/2,lower.tail = FALSE))## [1] 2.575829# p-value:
(Pval = pnorm(Zstat,lower.tail = FALSE)*2)## [1] 0.01241933# Actual confidence level:
((1-Pval)*100)## [1] 98.75807The calculations regarding the fast food example were repeated and continued to include a p-value. Recall that the null hypothesis stated that the population mean was equal to 4.5, and the test statistic under the null is equal to 2.5. The critical values marking the boundaries between the do not reject region and the reject regions was \(\pm 1.96\) for \(\alpha=0.05\) and \(\pm 2.58\) for \(\alpha=0.01\). Our test statistic falls inside the rejection region for \(\alpha=0.05\) and inside the nonrejection region for \(\alpha=0.01\). Our test statistic falls right on the boundary of a rejection and nonrejection region when \(p=0.0124\). This is the p-value of the problem. It states that you can reject the null hypothesis with at most 98.76% confidence and you will incur a 1.24% chance of being wrong. As expected, it is between 5% and 1% and gives you a tailor-made confidence interval for the hypothesis test at hand.
The definitions of a P-value
The p-value is the probability of getting a test statistic equal to or more extreme than the sample result, given that the null hypothesis \((H_0)\) is true.
While this is the technical definition of a p-value, it is a bit vague. There are some roughly equivalent definitions that might be easier to digest.
The p-value is the probability of committing a Type I error. If the p-value is greater than some arbitrarily given \(\alpha\), then you cannot reject the null.
The p-value is the probability that your null hypothesis is correct. The HIGHEST level of confidence at which you can reject the null is therefore \(1-p\).
This point touches on the idea of confidence in statistics. If you want me to make a statement with 100% confidence, then I’ll simply say anything can happen because it is a statement that has zero chance of being wrong.↩︎